この資料について
本資料ではシステム制御の学習や研究に必要な動的システムのシミュレーション手法について説明します.シミュレーション環境は基本的にMATLABを対象とします.
シミュレーションとは,ある現象をそれを模擬した装置や計算機を利用して擬似的に再現し,予測や評価に利用することといえます.最近ではデジタル計算機を用いた数値シミュレーションが一般的です. 数値シミュレーションを行うためには,現象の数学的モデルが必要になります.特に工学的な現象の場合,時間に関する微分方程式で表現できることが多いでしょう.その微分方程式を解くことができればシミュレーションが行えます.しかし,微分方程式の解析的な解(数式で表現される解)を求めることは一般的には難しいため,数値解(時間に対する数値の列)を求める手法が用いられます.
この資料ではまず,最も基本的なオイラー法やより精度の高いルンゲ・クッタ法による微分方程式の数値解法をMATLABでのスクリプト例を示しながら説明します.次に,システム制御では基本となる線形システムの状態空間表現について述べ,オイラー法やルンゲ・クッタ法でシミュレ-ションするMATLABスプリプトを示します. 最後に,MATLABのode45関数の利用方法について説明します.
オイラー法によるシミュレーション
一階常微分方程式
微分方程式とは,ある未知関数とその関数の導関数との関係が表されている方程式です.そのうち特に1変数の導関数で表されているものを常微分方程式といいます.システム制御に関わるシミュレーションでは時間に関する導関数で表される場合がほとんどでしょうから,常微分方程式が対象になります.さらに,導関数の階数(次数)が微分方程式の階数となります.
ということで,これから取り扱う最も簡単な微分方程式は以下のような一階の常微分方程式となります.ここで$x(t)$が未知関数,$x_0$はその初期値です.
$$\frac{dx(t)}{dt} = f(x(t), t) \ , \quad x(0) = x_0$$
もちろん実際の問題はより高階の常微分方程式が必要になりますが,この一階の微分方程式の数値解法を応用することで対応できます.
オイラー法
微分方程式の数値解法の基本は,ある時刻$t_k$から微少な刻み幅$\Delta t$(サンプリング時間またはサンプリング周期ともいう)だけ時間がたった後の関数値$x(t_k +\Delta t)$を逐次求めていくことです.これをいかに精度よく(できるだけ少ない計算量で)求めるかが数値解法の善し悪しと言えます.
オイラー法は以下のように$x(t_k +\Delta t)$のテイラー展開の最初の2項だけに基づきます.
$$ \begin{align*} x(t_k + \Delta t) &= x(t_k) + \frac{dx}{dt}\bigg|_{t=t_k} \Delta t + \frac{1}{2} \frac{d^2x}{dt^2}\bigg|_{t=t_k} \ \Delta t ^2 + \cdots \\ &\approx x(t_k) + \frac{dx}{dt}\bigg|_{t=t_k} \Delta t \\ &\approx x(t_k) + f(x(t_k), t_k) \Delta t \end{align*} $$
ここで,表記上の簡便性から,$x(t_k)$を$x_k$と表記することにし,$t_k +\Delta t$を$t_{k+1}$, $x(t_k +\Delta t)$を$x_{k+1}$などと表記することにします.この時オイラー法は以下のように表すことができます.
$$x_{k+1} = x_k + f(x_k, t_k)\Delta t$$
オイラー法による近似をグラフで示すと図のようになります.
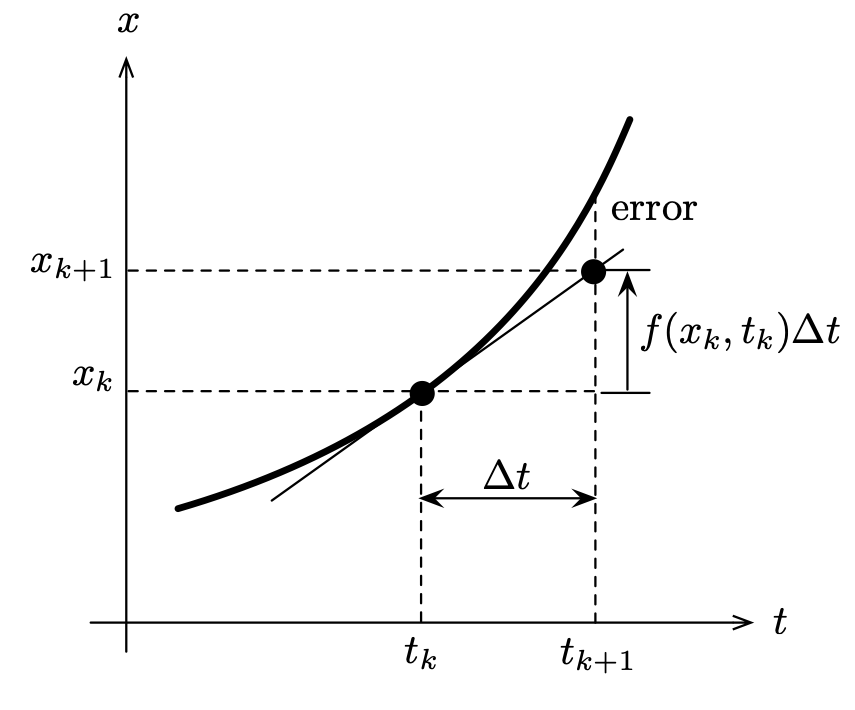
次のサンプリング時刻における$x(t)$の値,すなわち$x_{k+1}$を接線で一次近似して求めていると解釈できます.もとの微分方程式から,接線の傾きが$f(x_k, t_k)$ですから,それに$\Delta t$を乗じた物を$x_k$に加えることで$x_{k+1}$を求めています.図をみると誤差(error)が大きくて,本当に使えるのか心配ですが,$\Delta t$をできるだけ小さくすれば誤差を少なくできます.しかし,$\Delta t$を小さくすると,ある期間(例えば10秒間とか)のシミュレーションをするのにそれだけ計算回数が増えることになるので注意が必要です.
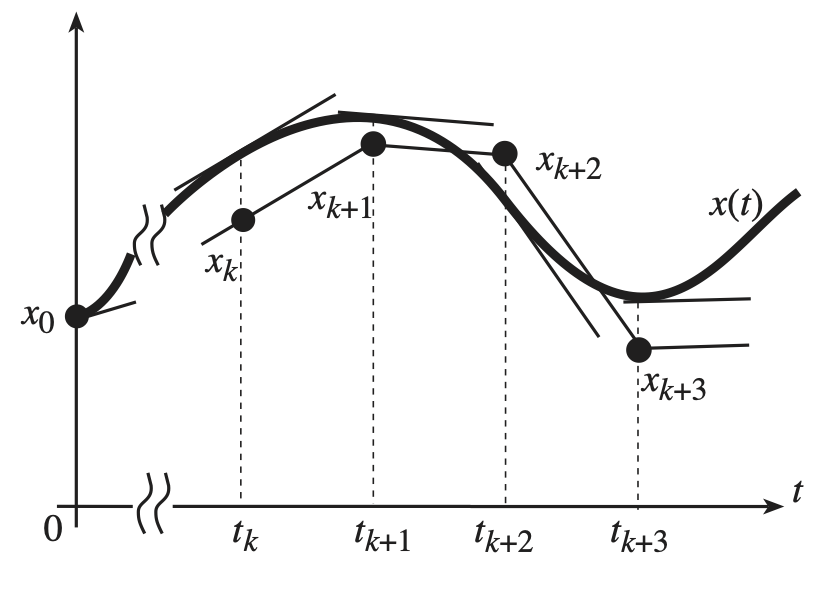
図では$x_k$が真値と一致している場合で書きましたが,実際はそうとも限りません.初期値$x_0$からスタートして,オイラー法を繰り返し使った近似計算は次図のようなイメージになります.$\Delta t$をできるだけ小さくとって,真値から離れすぎないようにする必要があります.なお,この図では近似のための接線を真値のグラフ$x(t)$に接するように引いていますが,$x_k$が真値からずれている場合は図の通りにはなりません.あくまでイメージです.
MATLABによる実現
次の微分方程式を例題に,MATLABでオイラー法によるシミュレーションを行うスクリプトを考えてみます.
$$\frac{dx}{dt} = - x + 1, \quad x_0 = 0$$
オイラー法を適用すれば
$$x_{k+1} = x_k +(-x_k + 1)\Delta t$$
とかけるので,繰り返しこの計算を行うMATLABスクリプトの例は以下のようになります.
- オイラー法による1階微分方程式のシミュレーション
dt = 0.01; % サンプリングタイム
x_k = 0; % xの初期値
x = []; % シミュレーション結果格納用変数
tim =[]; % シミュレーション時刻格納用変数
for t = 0 : dt : 10 % 時刻tは0から10までdt刻み
x_k1 = x_k + ( - x_k + 1) * dt ; % x_{k+1} の計算
x = [x x_k]; % xの末尾にx_kを追加
tim = [tim t]; % timの末尾にtを追加
x_k = x_k1; % 次回の計算のため x_{k} ← x_{k+1}に繰り上げ
end
plot(tim, x);
grid on;
axis([0 10 0 1.5]);
xlabel('time (s)');
ylabel('x');
MATLABにおける変数名の都合上,$x_k$をx_k,$x_{k+1}$をx_k1としています.
また,シミュレーション結果と時刻を格納する変数をそれぞれx,timとして用意し,x_kとtを行の末尾に追加しています.また,forループで繰り返す際に,次回の計算のために今回の$x_{k+1}$を次回の$x_k$として繰り上げておくことが必要です.
高次システムのシミュレーション
高次微分方程式の取り扱い
これまでは1階(次)の微分方程式を扱ってきましたが,現実には2次以上のシステムのシミュレーションが必要になることが多いと思います.その場合は,変数変換をすることで連立多元1階常微分方程式に変形して考えます.
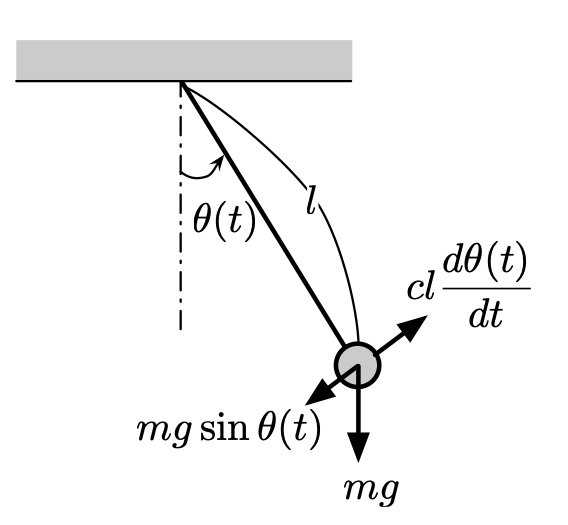
例えば,次のような微分方程式を考えます.これは,長さ$l$の軽い棒の先に質量$m$の重りがついた単振り子を初期角度$\theta_0$の位置から初速度0で放す状況を表しています(下図参照).ここで振り子は空気その他から速度に比例した抵抗を受けるものとし,その係数を$c$としています.
$$\frac{d^2 \theta(t)}{d t^2} = - \frac{g}{l} \sin \theta(t) - \frac{c}{m} \frac{d\theta(t)}{dt} \quad , \theta(0) = \theta_0 \quad , \frac{d\theta(t)}{dt} \bigg|_{t=0} = 0$$
このような2次のシステムの場合,次のような2個の変数を新たに定義します.これらを状態変数と呼びます.
$$ \begin{align*} x_1(t) &= \theta(t) \\ x_2(t) &= \frac{d \theta(t)}{dt} \end{align*} $$
状態変数を用いてもとの微分方程式を表すと以下のように1階の微分方程式が2本連立したものになります.
$$ \begin{align*} \dfrac{d x_1(t)}{dt} &= x_2(t) \quad , x_1(0) = \theta_0 \\ \dfrac{d x_2(t)}{dt} &= - \dfrac{g}{l} \sin x_1(t) - \frac{c}{m} x_2(t) \quad , x_2(0) = 0 \end{align*} $$
さらに,2つの状態変数を組にして,
$$ \boldsymbol{x}(t) = \begin{pmatrix}{c}x_1(t)\\x_2(t)\end{pmatrix} \quad , \boldsymbol{x}_0 = \begin{pmatrix}{c}\theta_0\\0\end{pmatrix} $$
のようにベクトル$\boldsymbol{x}(t)$で表現することで,最初の1階常微分方程式と同じ見た目になります.
$$ \frac{d \boldsymbol{x}(t)}{dt} = \boldsymbol{f}(\boldsymbol{x}(t), t) \quad , \boldsymbol{x}(0) = \boldsymbol{x}_0 $$
ここで,$\boldsymbol{f}(\boldsymbol{x}(t), t)$は以下となります.
$$ \boldsymbol{f}(\boldsymbol{x}(t), t) = \begin{pmatrix}x_2(t)\\ - \frac{g}{l} \sin x_1(t) - \frac{c}{m} x_2(t) \end{pmatrix} $$
オイラー法も形式的に次のように表すことができます.
$$ \boldsymbol{x}_{k+1} = \boldsymbol{x}_k + \boldsymbol{f}(\boldsymbol{x}_k, t_k) \Delta t $$
この状態変数表現に基づいたMATLABによるシミュレーション・スクリプトは次のようになります.
基本的には1次のシステムに対するオイラー法のスクリプトと同じですが,x_kやx_k1が2行×1列の列ベクトルになっていることが違いです.それに伴い,結果を格納する変数xが最終的に2行×サンプリング点数の行列になります.よって,シミュレーション結果として$\theta$だけをグラフ表示するには1行目だけを取り出す必要があり,そのため,plot関数の引数をx(1,:)としています.
なお,この例ではサンプリングタイム$\Delta t$を0.01秒としていますが,これを0.05秒にするとシミュレーション結果が大きく異なることに気がつくと思います.さらに$\Delta t$を大きくしていくと,それは誤差が大きくなるというようなレベルではなく,全く異なったシミュレーション結果になってしまいます.このようにサンプリングタイムの選択は重要で,基本的には十分小さくとる必要があります.
- オイラー法による単振り子のシミュレーション
dt = 0.01; % サンプリングタイム
m = 1; % 質量 1 kg
l = 0.5; % 振り子長さ 0.5 m
c = 0.5; % 空気抵抗係数
x_k = [30/180*pi ;
0 ]; % 初期角度30度, 初期速度0
x = []; % シミュレーション結果格納用変数
tim =[]; % シミュレーション時刻格納用変数
for t = 0 : dt : 10 % 時刻tは0から10までdt刻み
x_k1 = x_k + [ x_k(2) ;
-9.8/l * sin(x_k(1)) - c/m * x_k(2) ] * dt; % x_{k+1} の計算
x = [x x_k]; % xの末尾にx_kを追加
tim = [tim t]; % timの末尾にtを追加
x_k = x_k1; % 次回の計算のため x_{k} ← x_{k+1}に繰り上げ
end
plot(tim, x(1, :)); % x_1だけをグラフ表示
grid on;
axis([0 10 -1 1]);
xlabel('time (s)');
ylabel('\theta (rad)');
ルンゲ・クッタ法によるシミュレーション
2次のルンゲ・クッタ法(ホイン法)
オイラー法は$t_k$における導関数の値$f(x_k, t_k)$を使って$x_{k+1}$を近似していました.ここでは.より精度を高めるために,複数点における導関数の値を利用することを考えます.
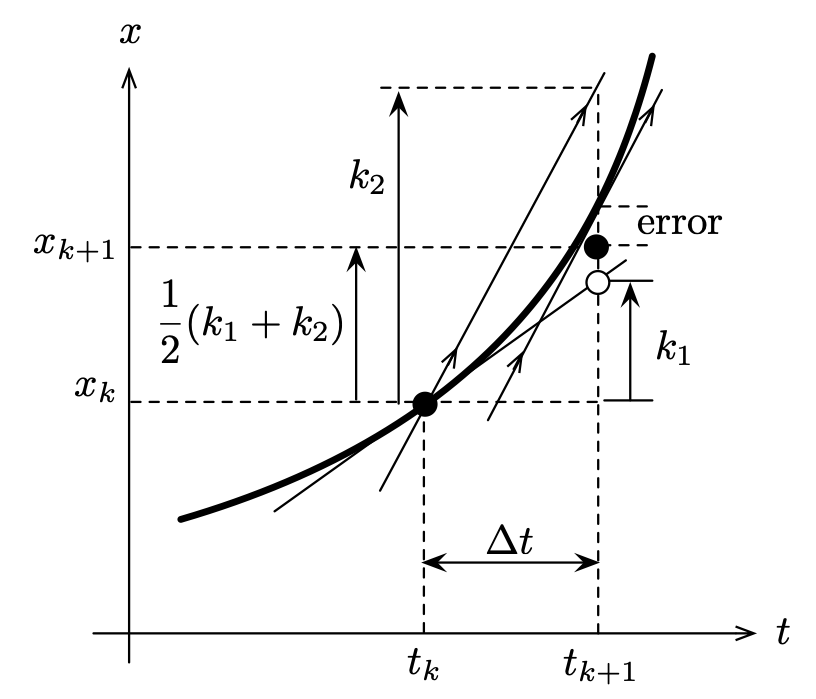
先の図のように$t_k$における接線の傾き$f(x_k, t_k)$だけを考えるのではなく,$t_{k+1}$における傾き$f(x_{k+1}, t_{k+1})$も利用して,それらの平均をその区間での傾きとして利用すれば,精度が高まりそうです.その場合,$x_{k+1}$は以下のように考えられます.
$$ x_{k+1} = x_k + \dfrac{1}{2} \left( f(x_k, t_k) + f(x_{k+1}, t_{k+1}) \right) \Delta t $$
しかし,$x_{k+1}$を求める計算に,$x_{k+1}$が含まれているのは無理があるので,$x_{k+1}$をオイラー法で近似した
$$ x_{k+1} = x_k + f(x_k, t_k)\Delta t $$
を代入すれば,
$$ x_{k+1} = x_k + \frac{1}{2} ( f(x_k, t_k) + f(x_k + f(x_k, t_k) \Delta t, t_{k+1}) ) \Delta t $$
とかけます.さらに,逐次計算しやすいように$k_1$,$k_2$という変数を定義して整理すれば,
$$ \begin{align*} k_1 &= f(x_k, t_k) \Delta t \\ k_2 &= f(x_k + k_1, t_{k+1}) \Delta t \\ x_{k+1} &= x_k + \frac{1}{2} ( k_1 + k_2 ) \end{align*} $$
となります.これは2次のルンゲ・クッタ法の一種で,ホイン法または修正オイラー法と呼ばれるものです.2次のルンゲ・クッタ法としては,導関数を取る点として区間の中点を考えた中点法と呼ばれるものもあります.
なお,オイラー法と同様に高階の微分方程式に対しても状態空間表現することでもちろん適用できます.
前節でオイラー法を用いてシミュレーションした1階の微分方程式をホイン法でシミュレーションするMATLABスクリプトは以下のようになります.微分方程式を複数回計算することになるので,関数fnc()として定義して利用していることに注意してください.
MATLABでユーザ関数を定義するには,functionとendとで定義式を囲み,関数名と同じ名前で拡張子が.mのファイル(この例だとfnc.m)として保存するか,同じスクリプトファイルの最後に記述するかのいずれかの方法をとります.ここでは同じスクリプトファイルに記述しています.
- ホイン法による1階微分方程式のシミュレーション
dt = 0.01; % サンプリングタイム
x_k = 0; % xの初期値
x = []; % シミュレーション結果格納用変数
tim =[]; % シミュレーション時刻格納用変数
for t = 0 : dt : 10 % 時刻tは0から10までdt刻み
k1 = fnc(x_k) * dt; % k1 の計算
k2 = fnc(x_k + k1) * dt; % k2 の計算
x_k1 = x_k + ( k1 + k2) / 2 ; % x_{k+1} の計算
x = [x x_k]; % xの末尾にx_kを追加
tim = [tim t]; % timの末尾にtを追加
x_k = x_k1; % 次回の計算のため x_{k} ← x_{k+1}に繰り上げ
end
plot(tim, x);
grid on;
axis([0 10 0 1.5]);
xlabel('time (s)');
ylabel('x ');
function xdot = fnc(x)
xdot = - x + 1 ;
end
次に2階の微分方程式をホイン法でシミュレーションする例を示します.この場合は$k_1$, $k_2$もベクトルになることに注意してください.
- ホイン法による単振り子のシミュレーション
dt = 0.01; % サンプリングタイム
x_k = [30/180*pi ;
0]; % 初期角度30度, 初期速度0
x = []; % シミュレーション結果格納用変数
tim =[]; % シミュレーション時刻格納用変数
for t = 0 : dt : 10 % 時刻tは0から10までdt刻み
k1 = fnc(x_k) * dt; % k1 の計算
k2 = fnc(x_k + k1) * dt; % k2 の計算
x_k1 = x_k + (k1 + k2) /2 ; % x_{k+1} の計算
x = [x x_k]; % xの末尾にx_kを追加
tim = [tim t]; % timの末尾にtを追加
x_k = x_k1; % 次回の計算のため x_{k} ← x_{k+1}に繰り上げ
end
plot(tim, x(1, :)); % x_1だけをグラフ表示
grid on;
axis([0 10 -1 1]);
xlabel('time (s)');
ylabel('\theta (rad)');
function xdot = fnc(x)
m = 1; % 質量 1 kg
l = 0.5; % 振り子長さ 0.5 m
c = 0.5; % 空気抵抗係数
xdot = [x(2);
-9.8/l * sin(x(1)) - c/m * x(2) ] ;
end
4次のルンゲ・クッタ法
2次のルンゲ・クッタ法では2点における導関数の値を使いました.同様に3点,4点と点数を増やしていくことで原理的には精度がよくなります.しかし実用上,4点を利用した4次のルンゲ・クッタ法で十分なようです.そのため,単にルンゲ・クッタ法というと4次の場合を指すことが多いです.
4次のルンゲ・クッタ法の計算手順は以下のようになります.
$$ \begin{align*} \boldsymbol{k}_1 &= \boldsymbol{f}(\boldsymbol{x}_k, t_k) \Delta t \\ \boldsymbol{k}_2 &= \boldsymbol{f}(\boldsymbol{x}_k + \frac{\boldsymbol{k}_1}{2}, t_k + \frac{\Delta t}{2}) \Delta t \\ \boldsymbol{k}_3 &= \boldsymbol{f}(\boldsymbol{x}_k + \frac{\boldsymbol{k}_2}{2}, t_k + \frac{\Delta t}{2}) \Delta t \\ \boldsymbol{k}_4 &= \boldsymbol{f}(\boldsymbol{x}_k + \boldsymbol{k}_3, t_{k+1}) \Delta t \\ \boldsymbol{x}_{k+1} &= \boldsymbol{x}_k + \frac{1}{6} ( \boldsymbol{k}_1 + 2 \boldsymbol{k}_2 + 2 \boldsymbol{k}_3 + \boldsymbol{k}_4) \end{align*} $$
先の単振り子のシミュレーションをルンゲ・クッタ法で計算するMATLABスクリプトを以下に示します.
- ルンゲ・クッタ法による単振り子のシミュレーション
dt = 0.01; % サンプリングタイム
m = 1; % 質量 1 kg
l = 0.5; % 振り子長さ 0.5 m
c = 0.5; % 空気抵抗係数
x_k = [30/180*pi ;
0 ]; % 初期角度30度, 初期速度0
x = []; % シミュレーション結果格納用変数
tim =[]; % シミュレーション時刻格納用変数
for t = 0 : dt : 10 % 時刻tは0から10までdt刻み
k1 = fnc(x_k) * dt; % k1 の計算
k2 = fnc(x_k + k1/2) * dt; % k2 の計算
k3 = fnc(x_k + k2/2) * dt; % k3 の計算
k4 = fnc(x_k + k3) * dt; % k4 の計算
x_k1 = x_k + (k1 + 2 * k2 + 2 * k3 + k4 ) /6 ; % x_{k+1} の計算
x = [x x_k]; % xの末尾にx_kを追加
tim = [tim t]; % timの末尾にtを追加
x_k = x_k1; % 次回の計算のため x_{k} ← x_{k+1}に繰り上げ
end
plot(tim, x(1, :)); % x_1だけをグラフ表示
grid on;
axis([0 10 -1 1]);
xlabel('time (s)');
ylabel('\theta (rad)');
function xdot = fnc(x)
m = 1; % 質量 1 kg
l = 0.5; % 振り子長さ 0.5 m
c = 0.5; % 空気抵抗係数
xdot = [x(2);
-9.8/l * sin(x(1)) - c/m * x(2) ] ;
end
MATLAB関数を利用したシミュレーション
ode45関数の使用方法
ルンゲ・クッタ法を用いれば比較でき大きなサンプリングタイムでも精度良くシミュレーションができます.しかし,それでも大き過ぎれば精度は落ちますし,場合によっては発散してしまうこともあります.かといってサンプリングタイムを不必要に小さくすると計算時間が非常に長くなってしまいます.
MATLABにはode45()という関数が用意されています.これは指定した精度に応じてサンプリングタイムを自動的に加減してくれます.しかもサンプリングタイムは一定ではなく,シミュレーション中に必要に応じて小さくなったり大きくなったりします.精度はデフォルトで決まっていますが,オプションとして指定することも可能です.詳しくはode45関数のマニュアルを参照してください.
先の単振り子の自由応答のシミュレーションをode45関数を使って求めるスクリプト例を示します.
- ode45関数を使った単振り子のシミュレーション1
x0 = [pi/6;
0];
tspan = [0 10]; % 時間範囲の指定
[t, x] = ode45(@fnc, tspan, x0);
plot(t, x(:, 1));
grid('on');
axis([0 10 -1 1]);
xlabel('time (s)');
ylabel('\theta (rad)');
% 導関数の定義
function xdot = fnc(t, x)
m = 1;
l = 0.5;
c = 0.5;
xdot = [x(2);
-9.8/l*sin(x(1))-c/m*x(2)];
end
ode45関数を利用したスクリプトのポイントは以下のようになります.
- 導関数は時刻
tと状態量xをこの順番で引数とする関数として定義する必要があります.$t$を省略することもできません. - 定義した導関数の関数名に@マークをつけてode45関数の引数として指定します.
- シミュレーションの時間範囲を,変数
tspanで開始時刻と終了時刻の2要素の行ベクトルとして指定します. - サンプリングタイムは自動的に設定されるため,あらかじめ指定する必要はありません.
- サンプリングタイムは一定ではなく,必要に応じて可変となります.そのため,出力されるシミュレーション結果の状態量
xは一定サンプリングではないので注意が必要です.グラフ化する時は同時に出力されるベクトルtとペアにする必要があります. - 状態量ベクトルの初期値は列ベクトルで指定しますが,出力される状態量
x状態変数が横に並び,時系列に沿って縦長のベクトルになるので注意が必要です.よって特定の状態量だけをプロットするときには列方向に切り出す必要があります.